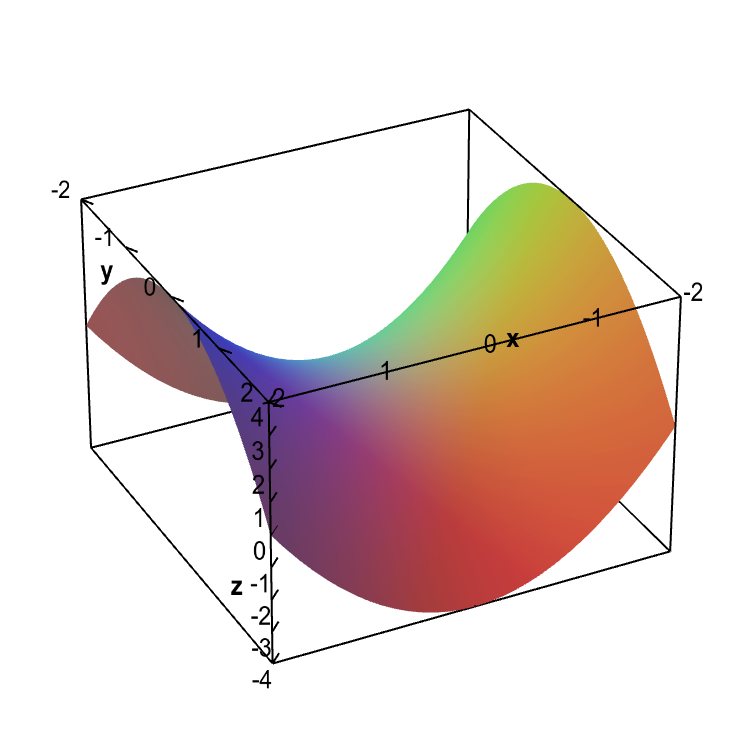Ace Tips About What Is A Hyperbolic Curve Dash Plotly Line Graph

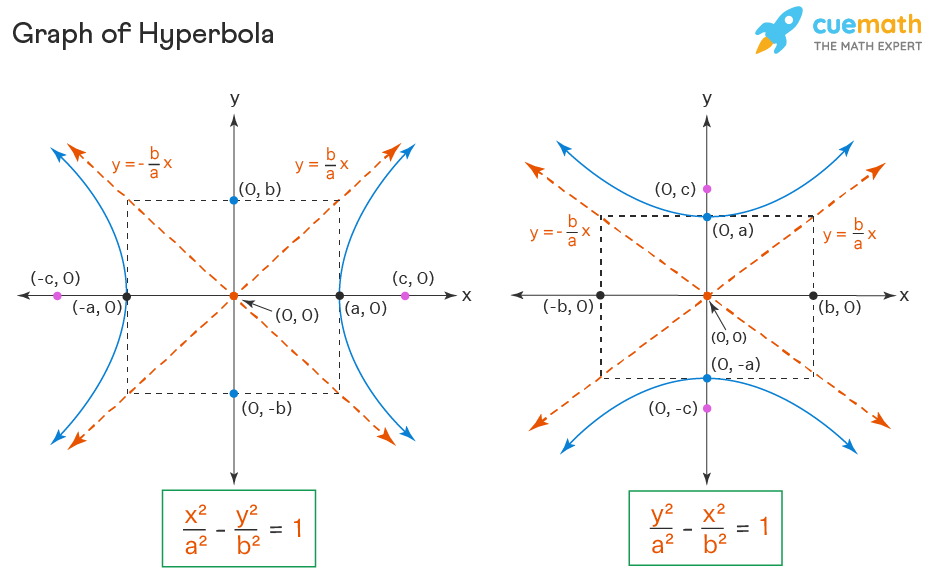
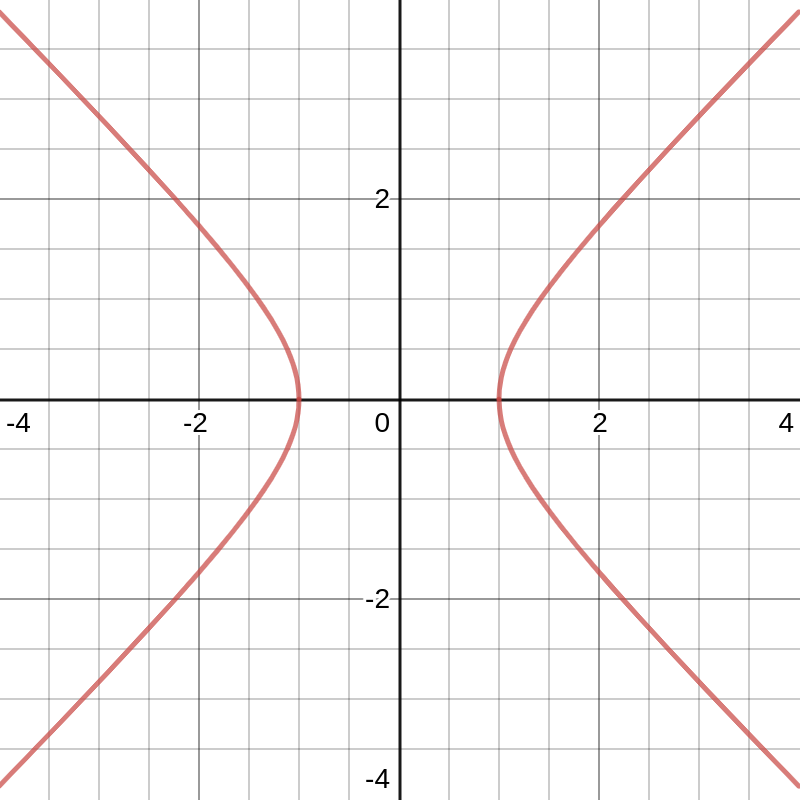
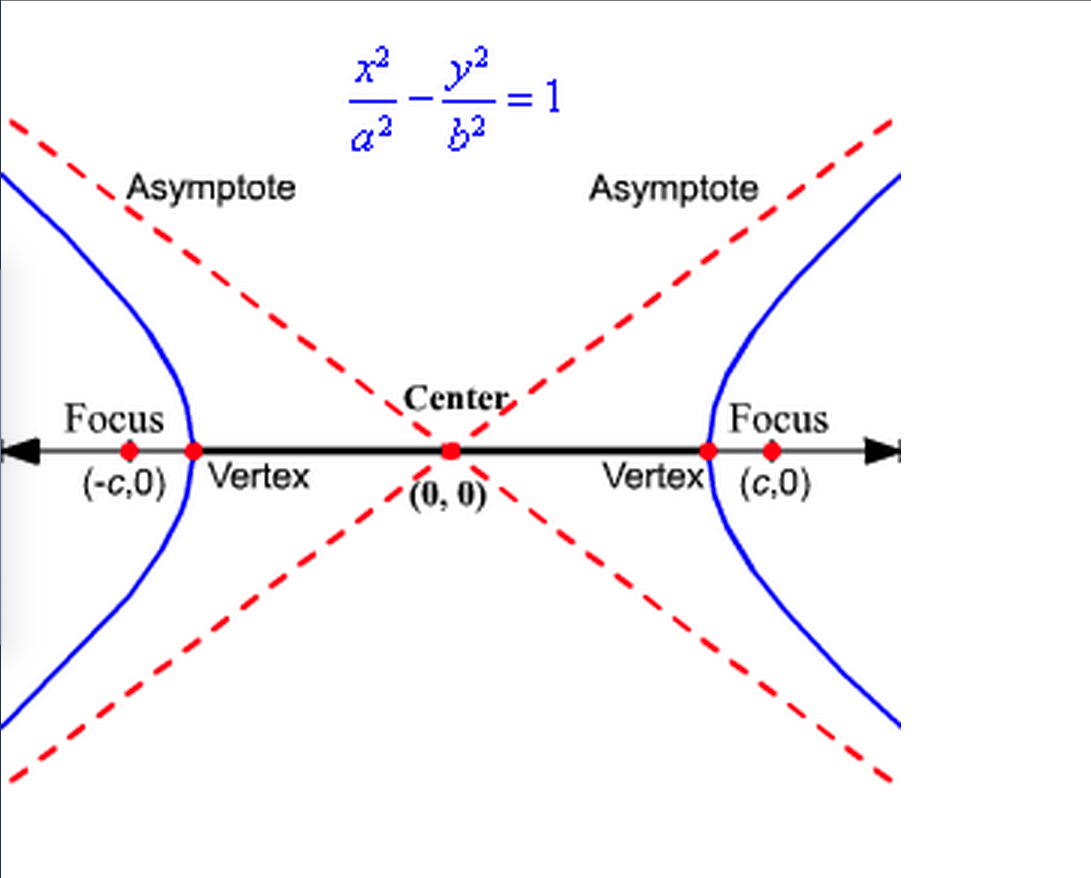
An hyperbola looks sort of like two mirrored parabolas, with the two halves being called branches.

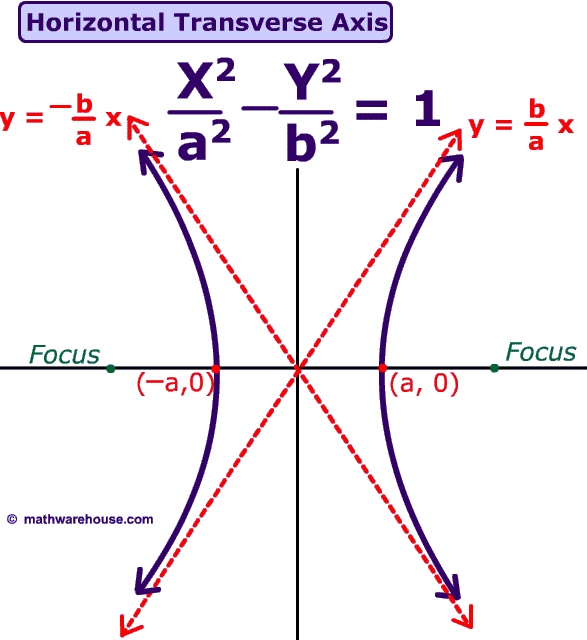
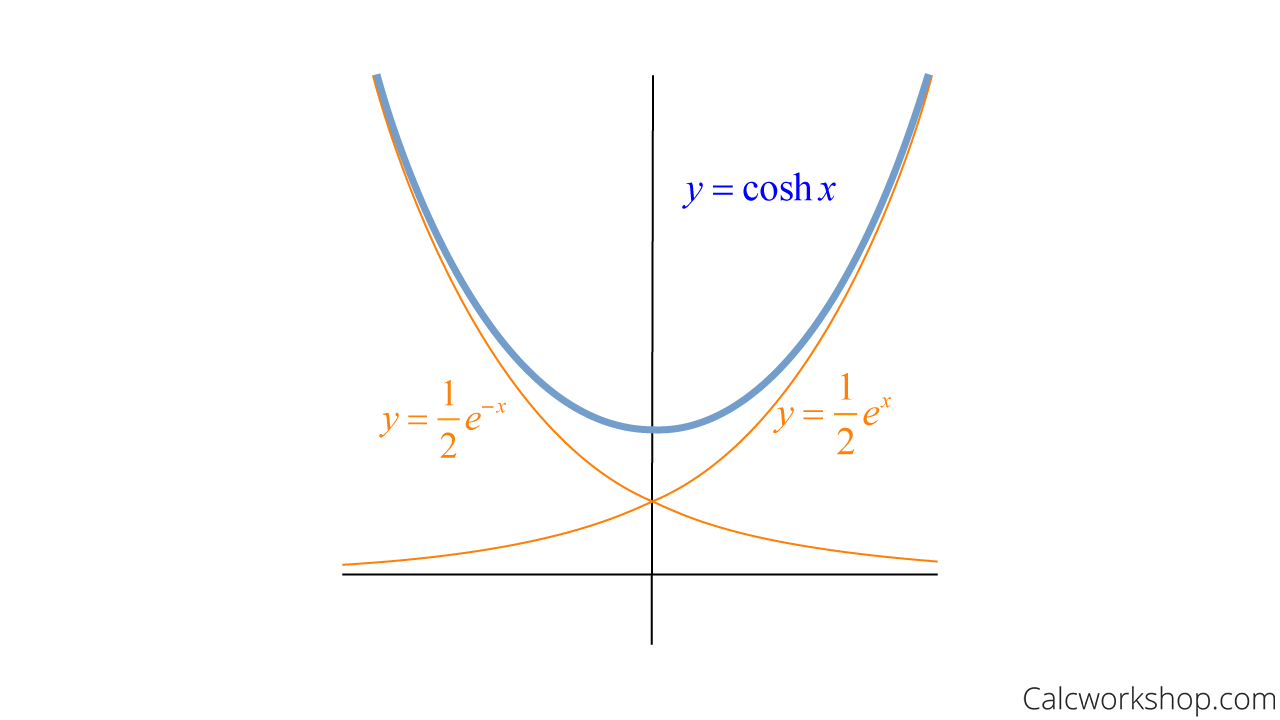
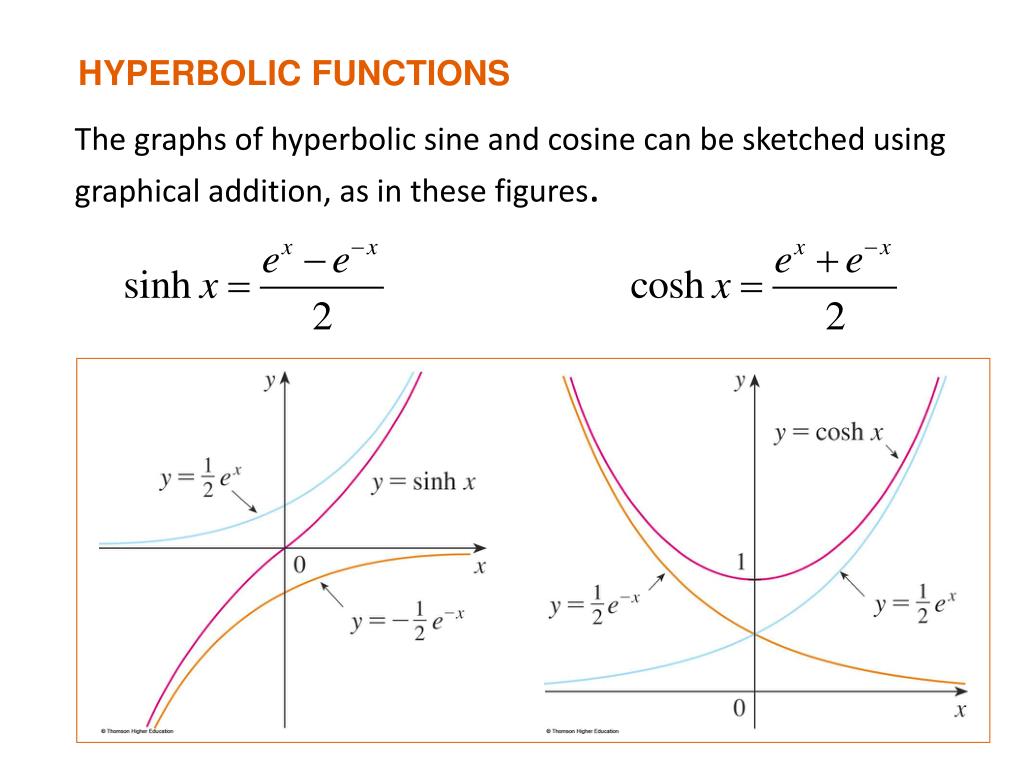
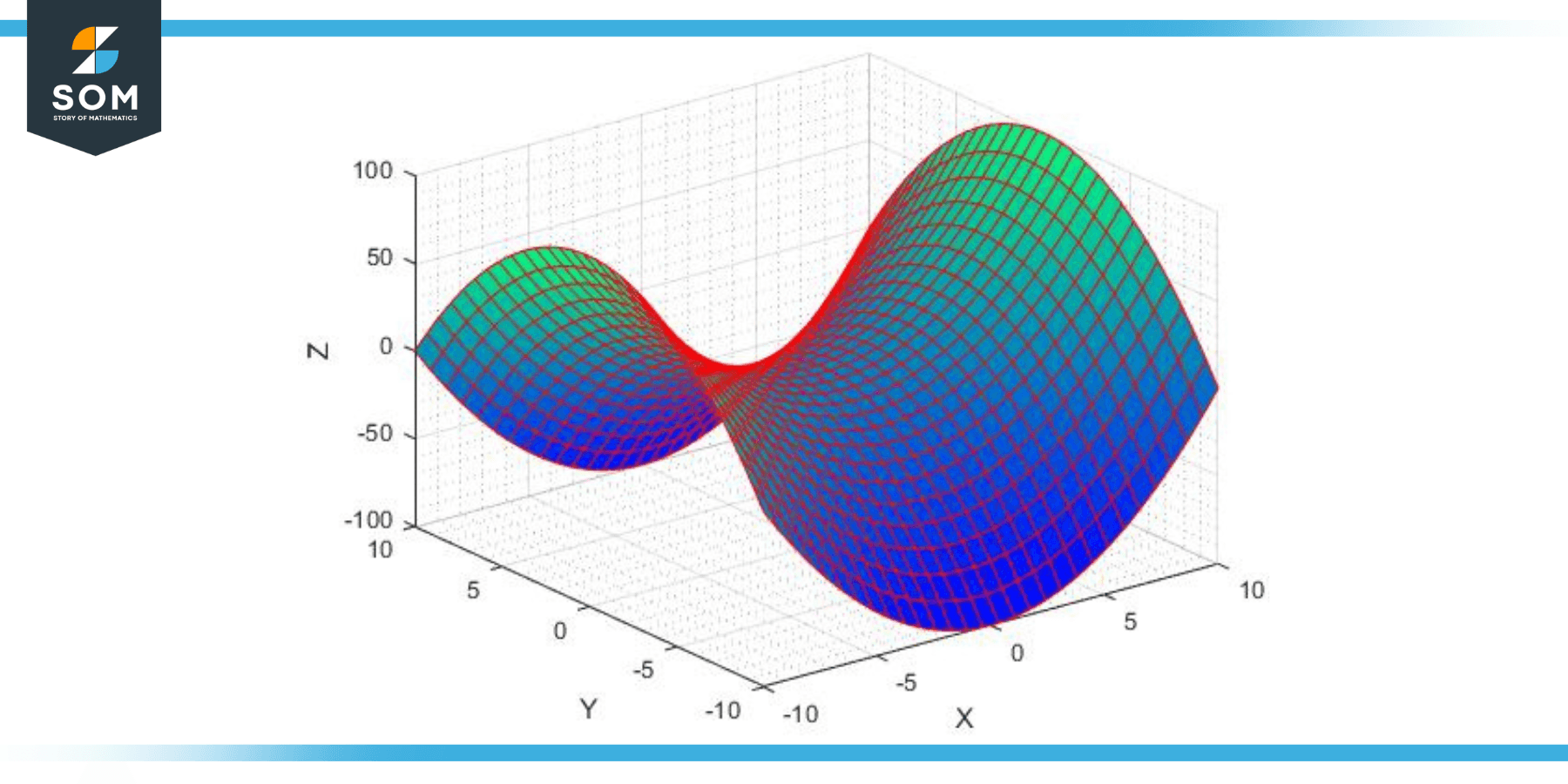
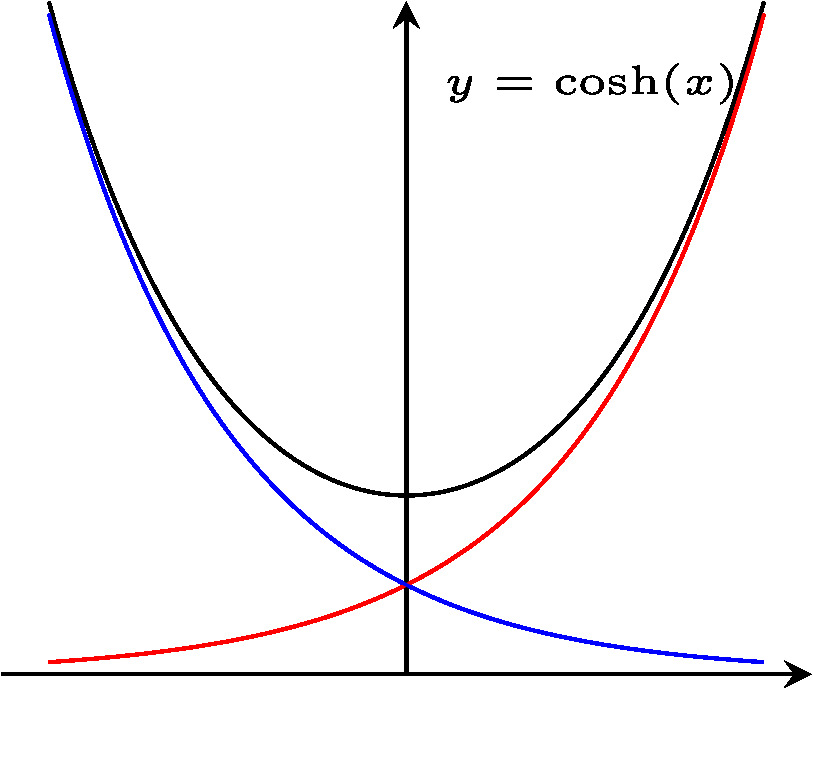
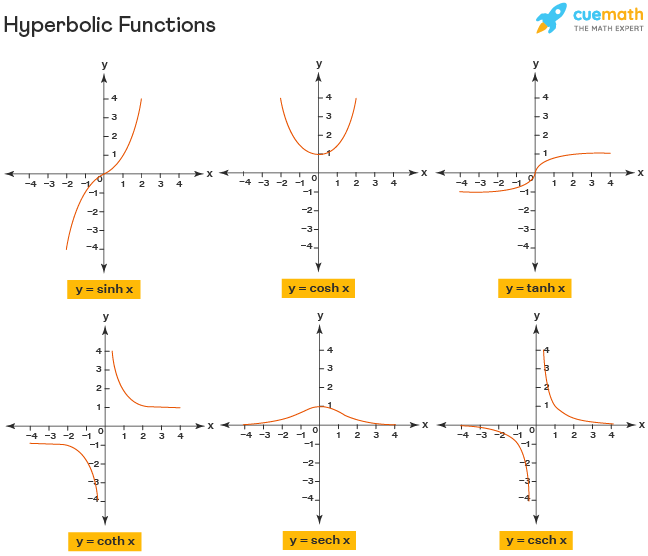
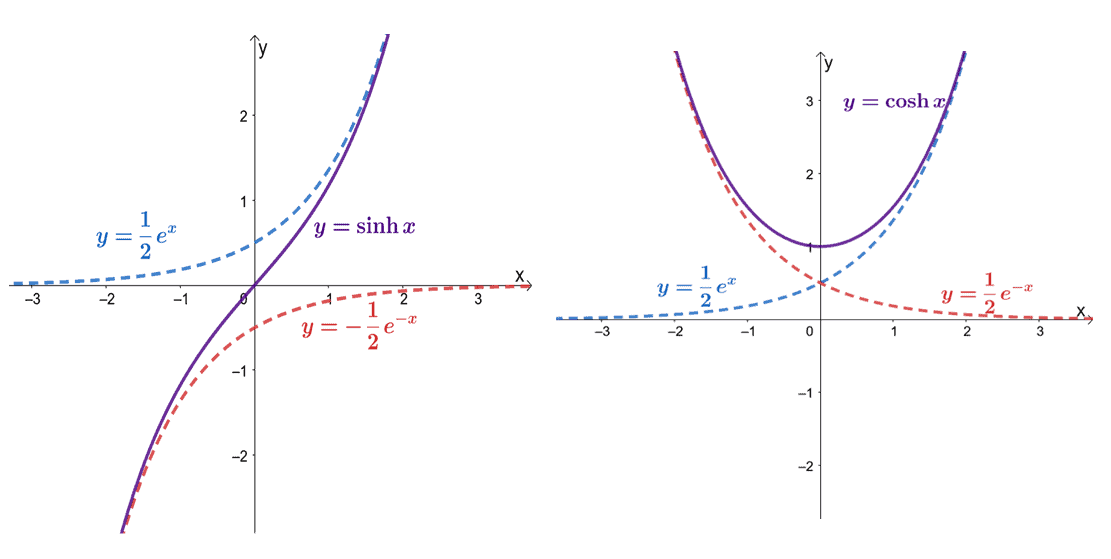
What is a hyperbolic curve. Definition 4.11.1 the hyperbolic cosine is the function coshx = ex + e − x 2, and the hyperbolic sine is the function sinhx = ex − e − x 2. Parabola is the locus of all points, which are equally spaced from a fixed line (called directrix) and a fixed point (called the focus). A hyperbola, a type of smooth curve lying in a plane, has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows.

One of the most known examples of an object that can be modeled by a hyperbolic function is a catenary. The parallel postulate of euclidean geometry is replaced with: Hyperbolic rays in the kagome metal csv 3 sb 5.

In mathematics, a hyperbola (/ h aɪ ˈ p ɜːr b ə l ə / ⓘ; Theta is its own unique symbol in mathematics. It is two curves that are like infinite bows.

How does this relate to a hyperbola, which is an algebraic curve? The hyperbolic functions satisfy the following identities: Hyperbola is defined as an open curve having two branches which are mirror images of each other.

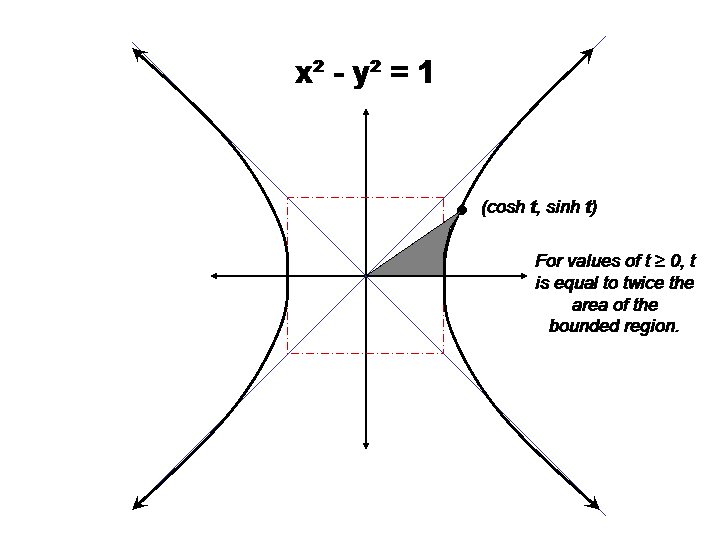
This is the curve formed when a rope, chain, or cable is suspended. The identity cosh2x − sinh2x = 1 was proved when deriving the coordinates of points on the unit hyperbola x2 − y2 = 1 in terms of the hyperbolic angle (since such a point (x, y) = (cosha, sinha) must satisfy x2 − y2 = 1 ). An hyperbola is one of the conic sections.

If the exponential function $e^x$ is water, the hyperbolic functions ($\cosh$ and $\sinh$) are hydrogen and oxygen. A hanging cable forms a curve called a catenary defined using the cosh function: Just like one of its conic partners, the ellipse, a hyperbola also has two foci and is defined as the set of points where the absolute value of the difference of the distances to.

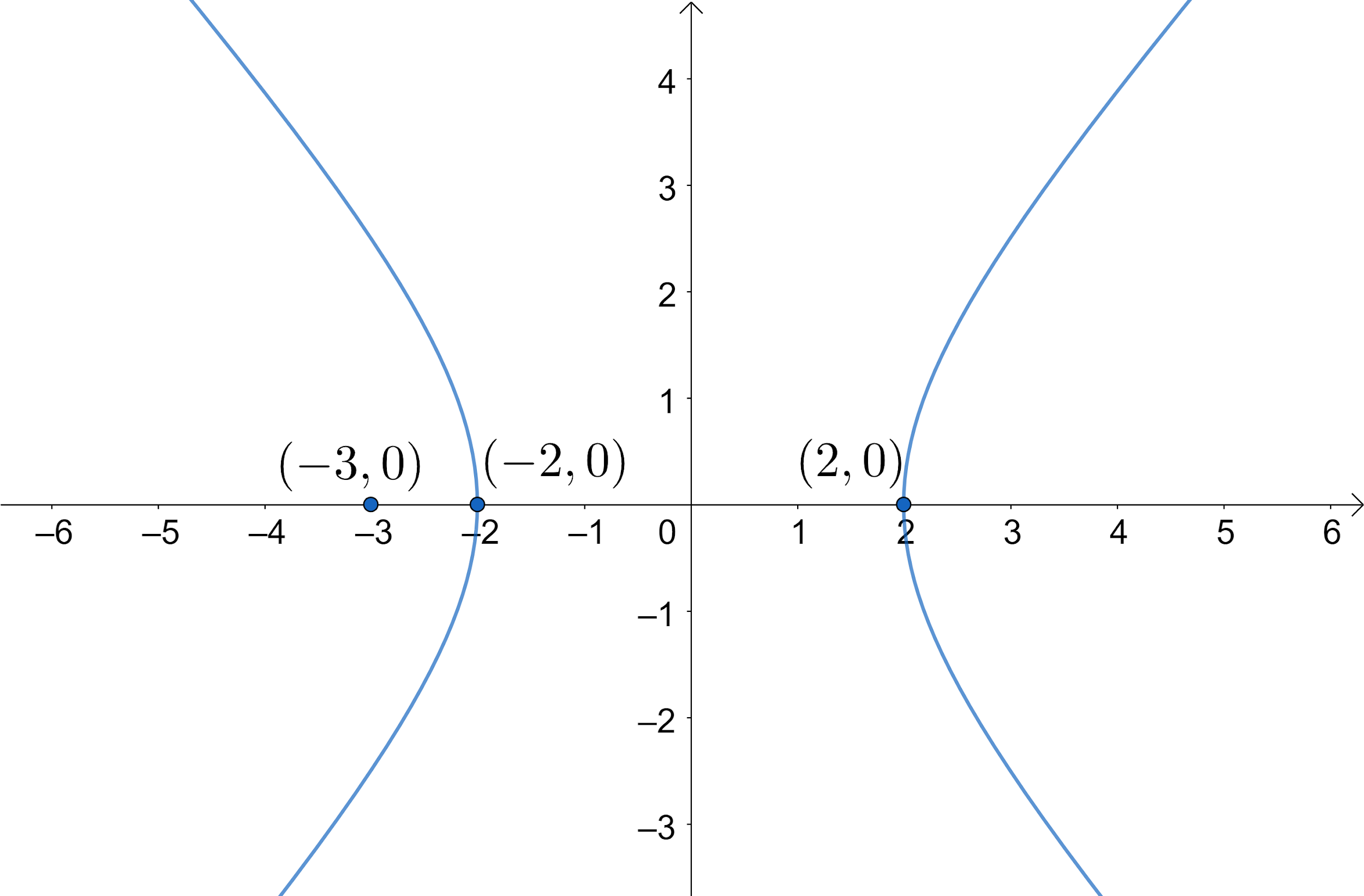
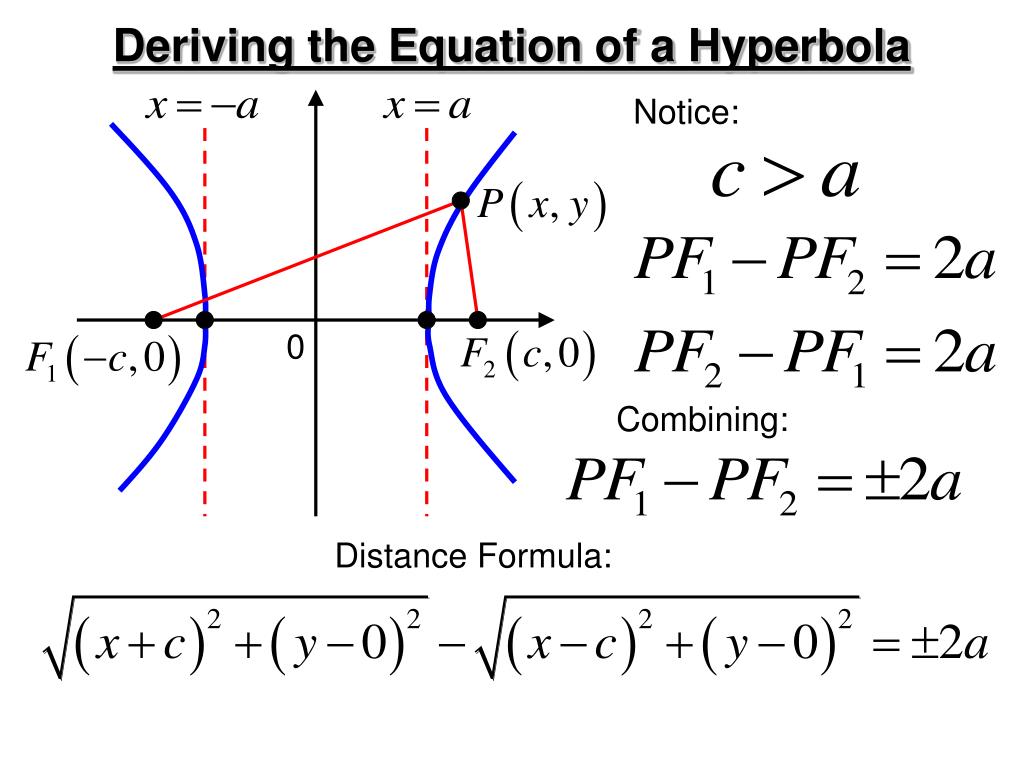
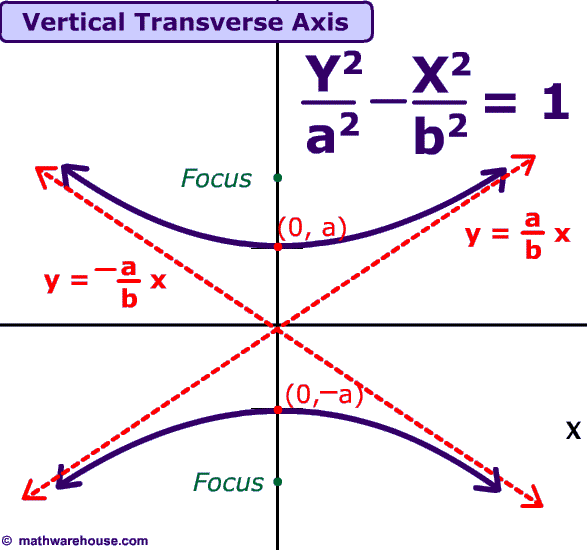
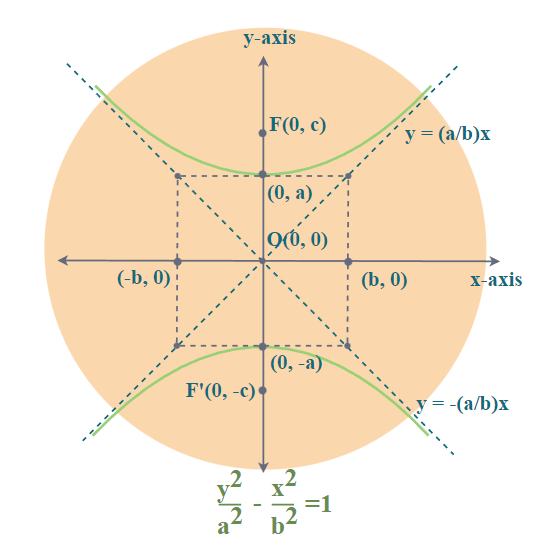
Sal introduces the standard equation for hyperbolas, and how it can be used in order to determine the direction of the hyperbola and its vertices. Any branch of a hyperbola can also be defined as a curve where the distances of any point from: A hyperbola is the locus of all those points in a plane where the difference in their distances from two fixed points in the plane is constant.

A fixed straight line (the directrix) are always in the same ratio. This is a bit surprising given our initial definitions. The hyperbolic function occurs in the solutions of linear differential equations, calculation of distance and angles in the hyperbolic geometry, laplace’s equations in the cartesian coordinates.

The hyperbolic functions appear with some frequency in applications, and are quite similar in many respects to the trigonometric functions. Here, we will study the hyperbola equation, foci, eccentricity, directrix, latus rectum and characteristics of such curves. Cosumnes river college.

Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. It takes the form of two branches that are mirror images of one another that together form a shape similar to a bow. One of the interesting uses of hyperbolic functions is the curve made by suspended cables or chains.