Fun Tips About How To Compare 3 Groups Statistically Excel Chart With Multiple Lines

For normally distributed data we can use anova to compare the means of the groups.

How to compare 3 groups statistically. However, there was no difference in potassium levels when comparing groups 1 and 3. What complicates this of course is that. Instead, you probably want to look at whether the group means are.

I'd also note that the. A statistical analysis for comparing three or more data sets depends on the type of data collected. However, if the 3 groups are separate, it doesn't make sense to compare single observations.

We will need to know, for. One or more groups’ means differ from the others. Anova test for equality of all means.

Sometimes your research hypothesis may predict that the size of a regression coefficient may vary across groups. I created a dataframe to compare the proportions of three or more groups (real data has more than 50,000 rows). I would simply calculate odds (or risk) ratios between group a and b, between b and c, and between a and c and see if they statistically different.

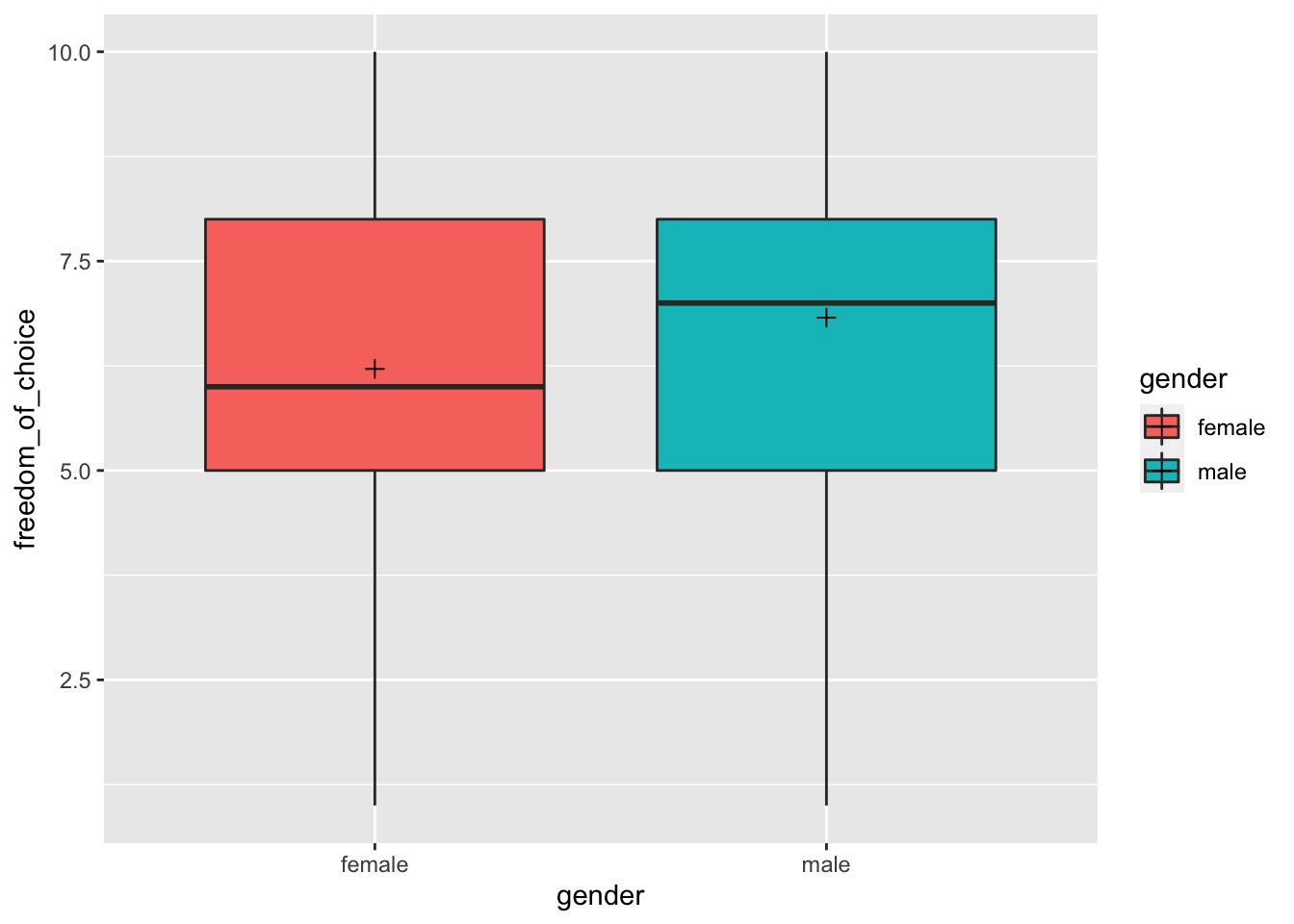
Put your 3 groups in columns, and ride the tube: The t test compares the difference between two means and compares that difference to the standard error of the difference, computed from the standard deviations and. Analysis of variance (anova) tests.

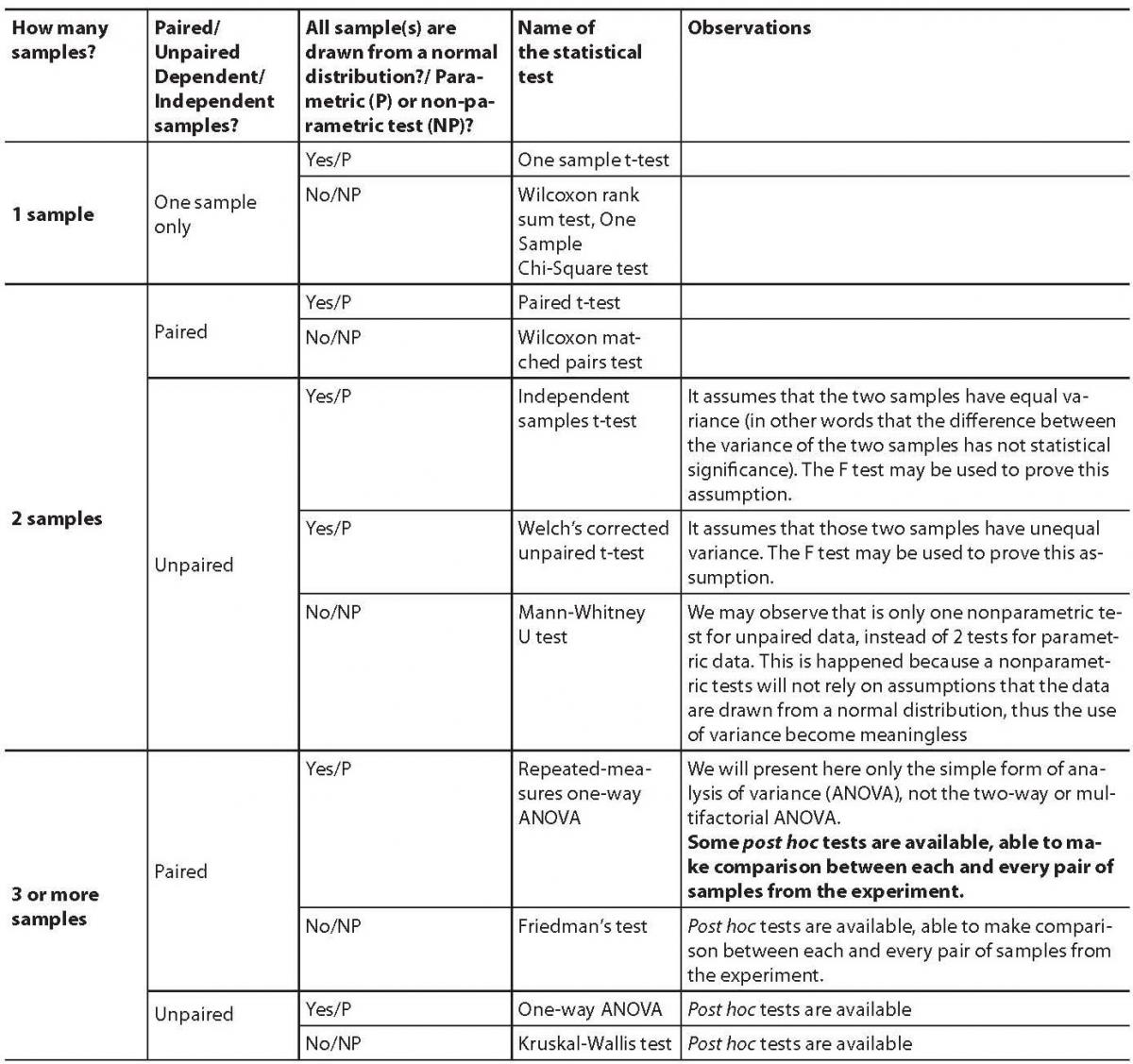
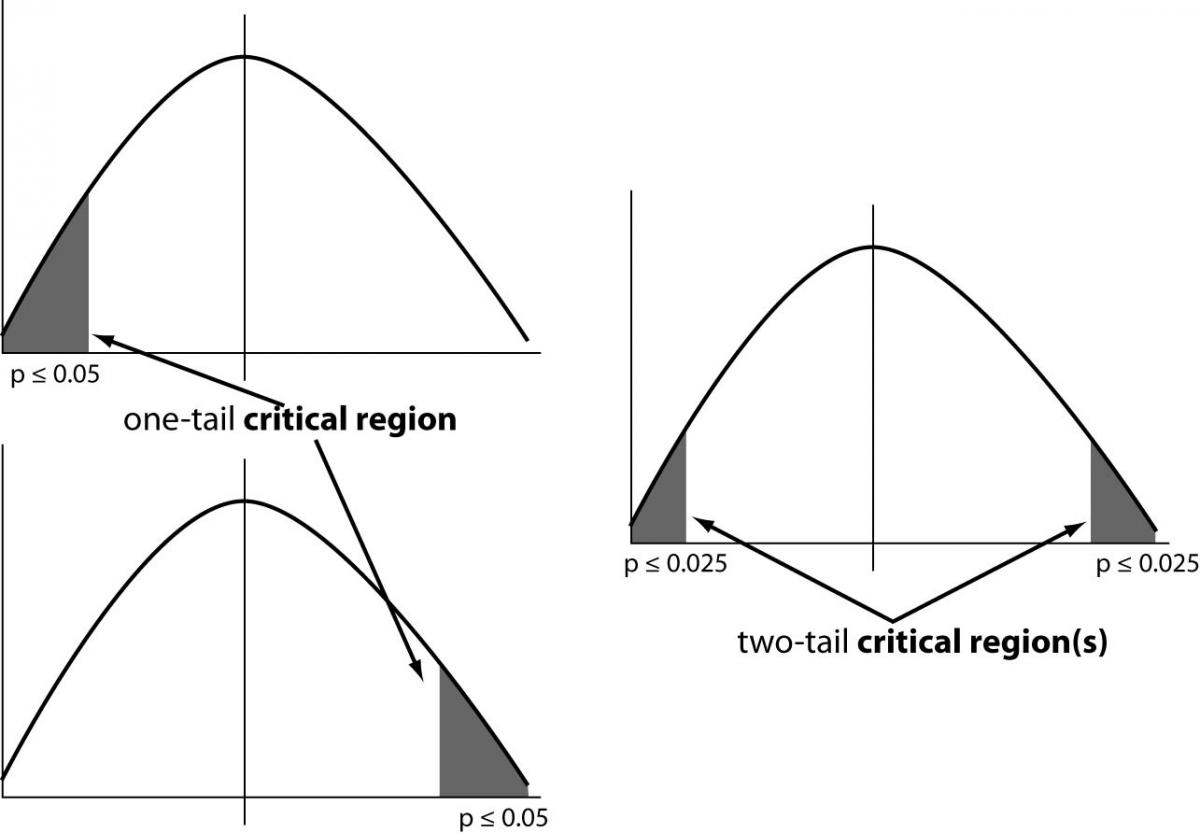
This article will present a step by step guide about the test selection process used to compare two or more groups for statistical differences. Multiple comparisons make simultaneous inferences about a set of parameters. Sample groups’ means are equal.

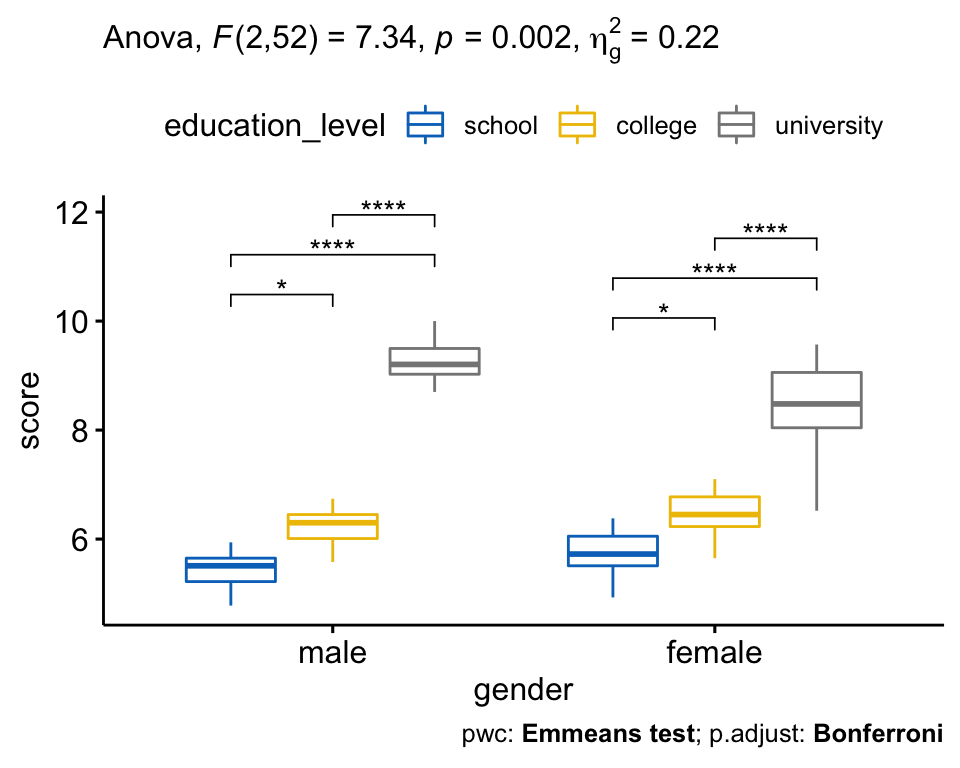
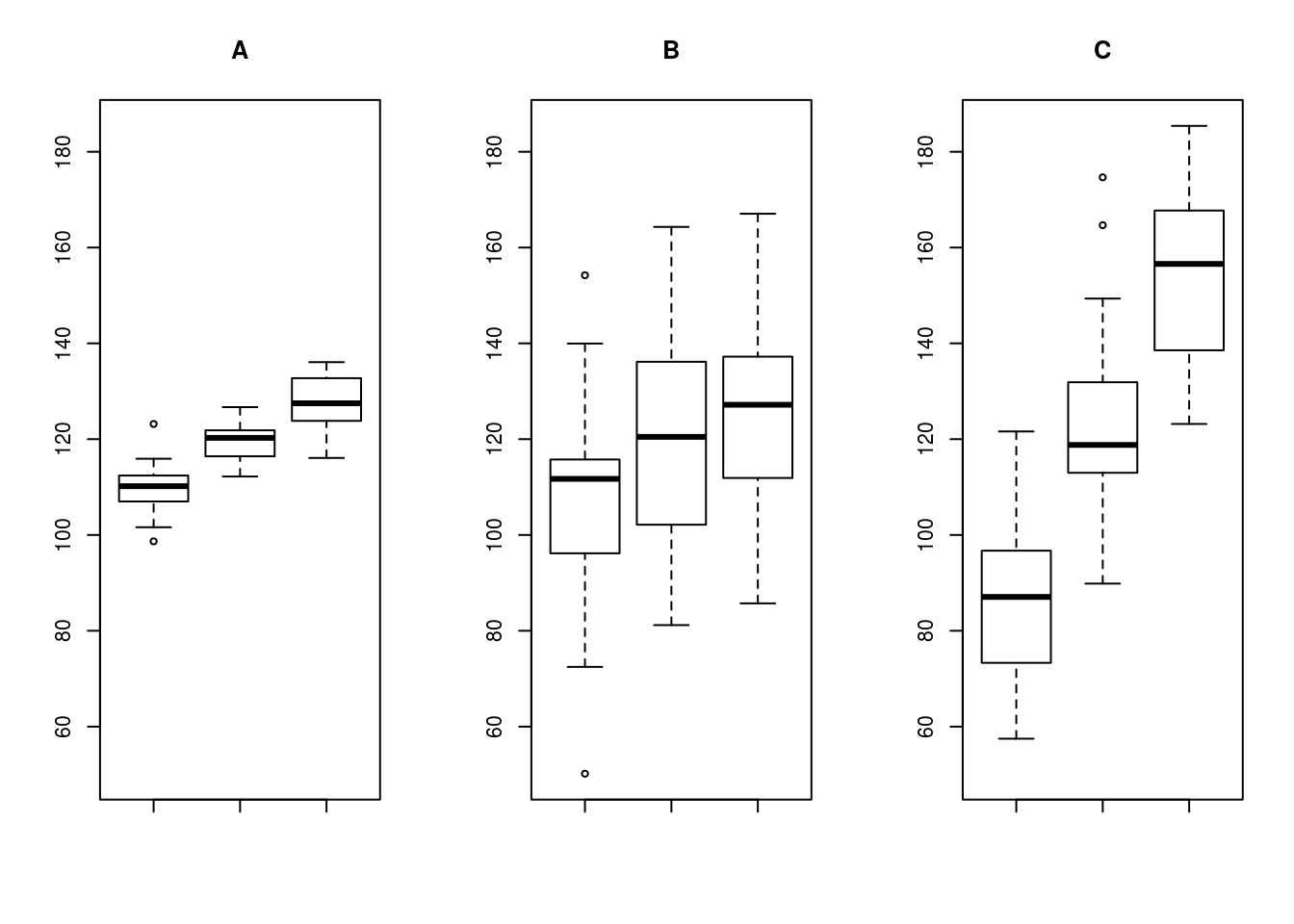
I will like to perform and statistical comparison between 3 groups, in order to determine if statistically they are different or not. We will use analysis of variance (anova) to find out if the difference between three mean scores is statistically significant. If the data are normally distributed, you should use an one way anova analysis.

What statistical test should i use if i have three independent groups of interval data and would want to check whether their means are significantly different? We may formulate four null hypotheses to compare the group means μ1, μ2, and μ3. My data for all of the 3 groups follows.

In the left column, 0 indicates survival, 1 indicates death, and 0,1,2,3 in the right column indicates the grade. For example, you might believe that the regression coefficient. Each statistical test has certain assumptions that must be met for.

Which statistics would be ideal for comparing two groups with three unpaired data points in each group? A common problem that arises in research is the comparison of the central tendency of one group to a value, or to another group or groups. I don't see a reason to do a.