Top Notch Tips About What Is A Curved Function Called Plot Online Free

A curved line is a fundamental concept in mathematics and geometry.

What is a curved function called. This is the definition that appeared more than 2000 years ago in euclid's elements: Intuitively, a curve may be thought of as the trace left by a moving point. It is a line that consistently deviates from straightness, bending or curving in various ways.

What would this curve be. As the name suggests, unit tangent vectors. Loosely speaking, the word curve is often used to.

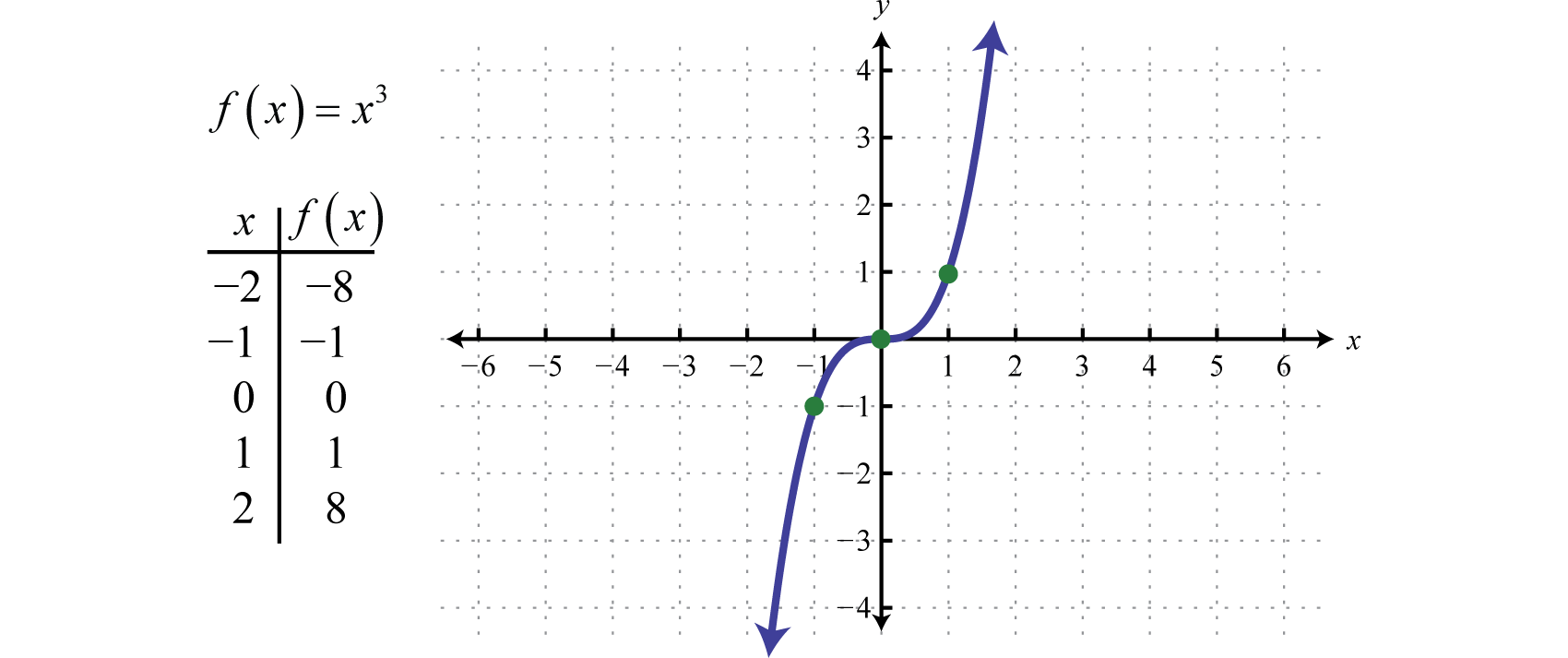
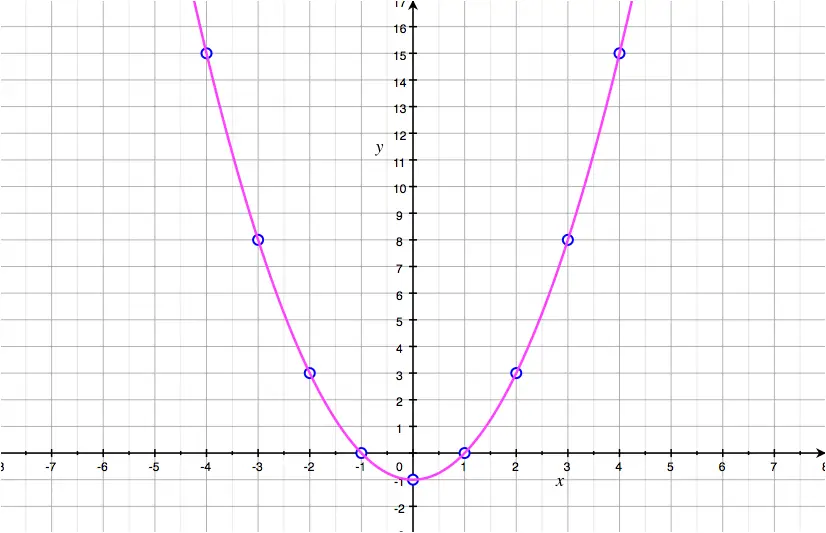
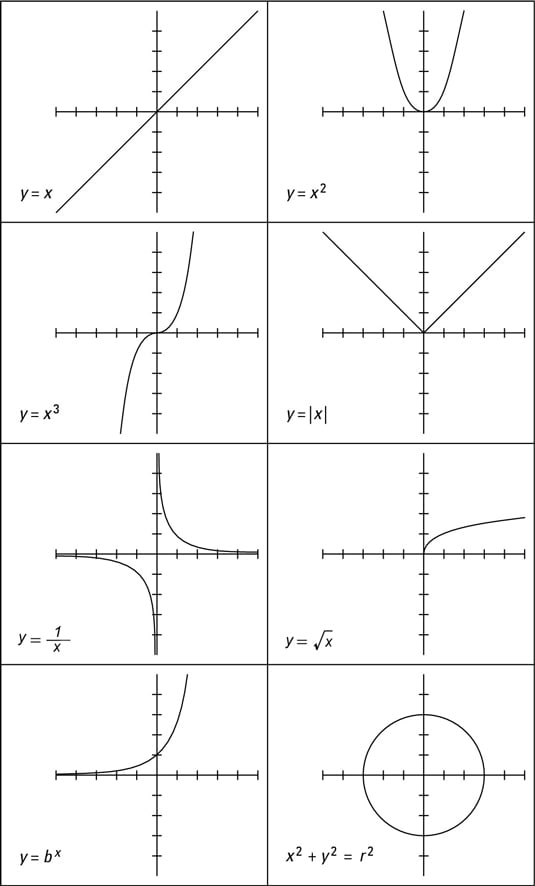
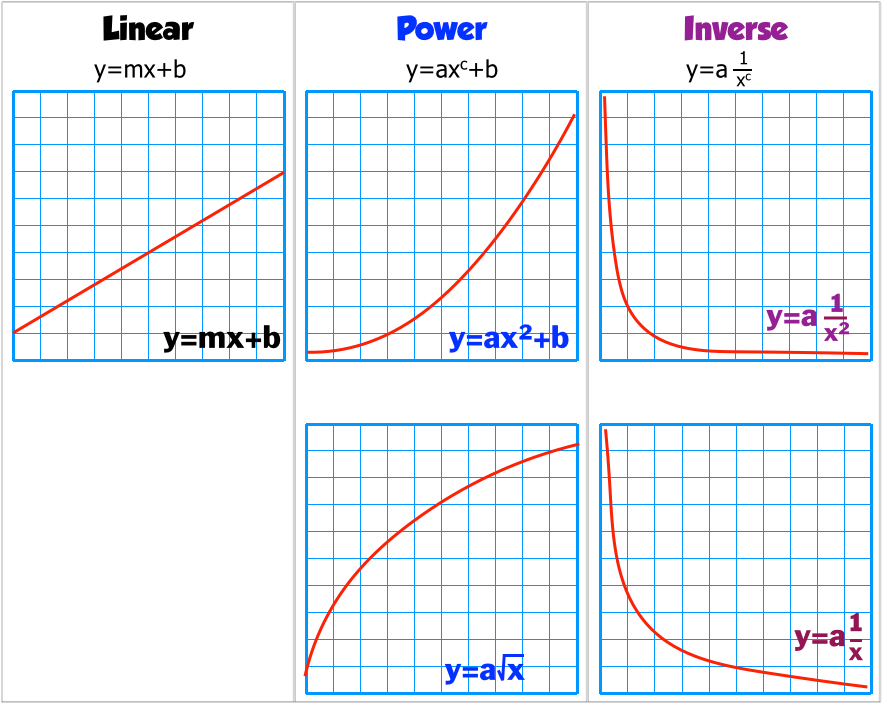
This is a list of wikipedia articles about curves used in different fields: A curve is a continuous line that flows smoothly and without abrupt turns. A function \(f(x)\) can be illustrated by its curve on an \(xy\) grid.

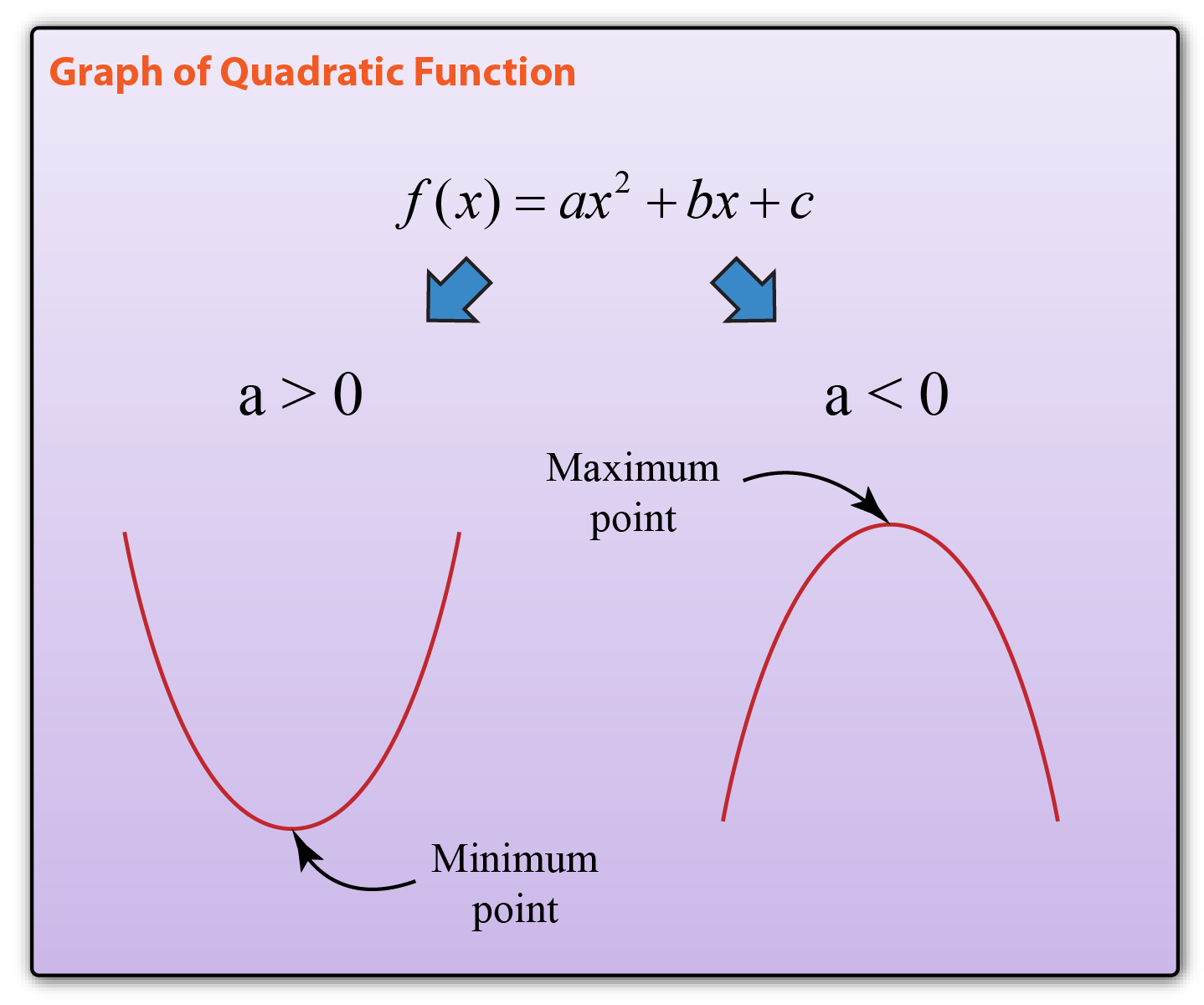
Κ = | | d t d s | |. In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. A curve in mathematics is a line or a shape that is smoothly traced in a plane and has a bent or arc in it.

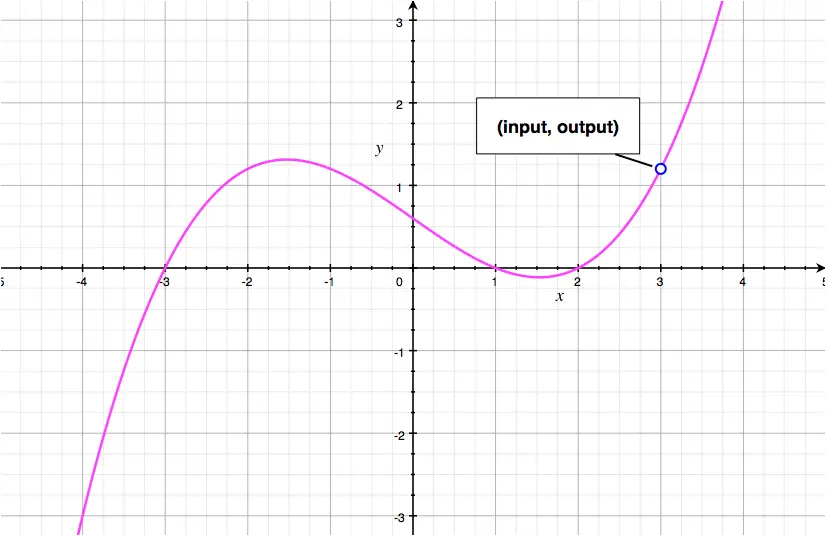
A curved line is a type of line that is not straight and is bent. A curve can be identified easily by observing if it bends and modifies its course at least once. This allows us to see all of the input/output values of a function with a single curve.

A curve is a continuous function $\gamma: A curved line is defined as a line that is not straight but is bent. Given a domain , a function 's.

It is continuous and smooth, without any sharp turns. So, every curve is a function, but this does not means that, if $x= \mathbb{r}^2$ than any curve can be expressed as a. Learn about curved shapes, types of curves, examples, facts, and more.

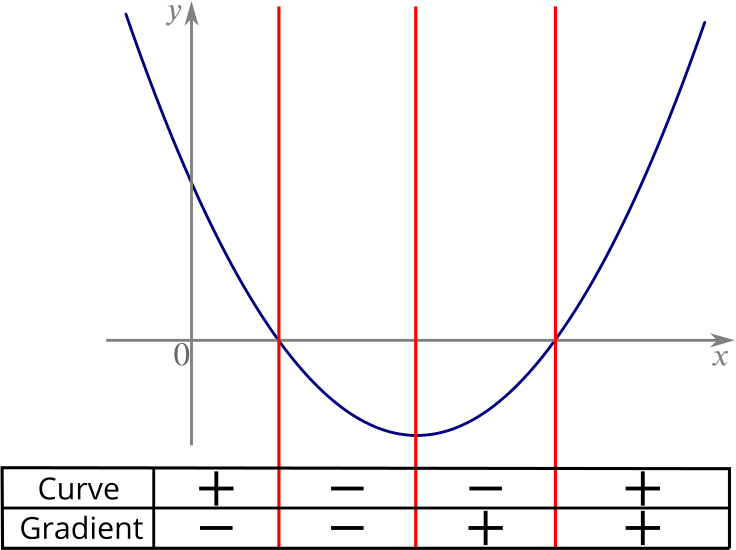
Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the. In formulas, curvature is defined as the magnitude of the derivative of a unit tangent vector function with respect to arc length: In other words, curved lines are a form of a line that.

In other words, a curve is defined as a group of points that resemble a straight line that. I \to x$ where $ i \subset \mathbb{r}$ is an interval and $x$ is a topological space. Very often when differential topologists and geometers speak of a curve, they mean an image of a regular path.

Don't worry, i'll talk about. Before learning what curvature of a curve is and how to find the value of that curvature, we must first learn about unit tangent vector. Ideally, it is smooth and continuous.