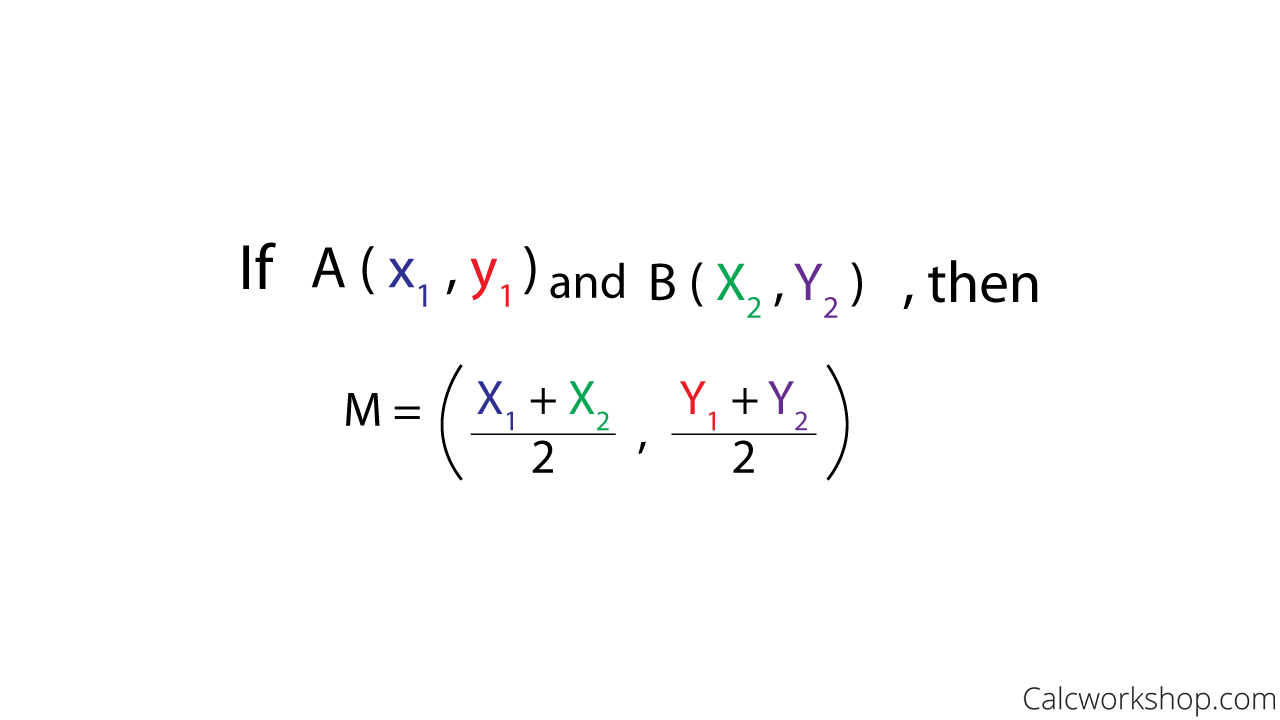One Of The Best Info About How Do You Integrate A Line Segment Dynamic Graph

Full vector calculus playlist:
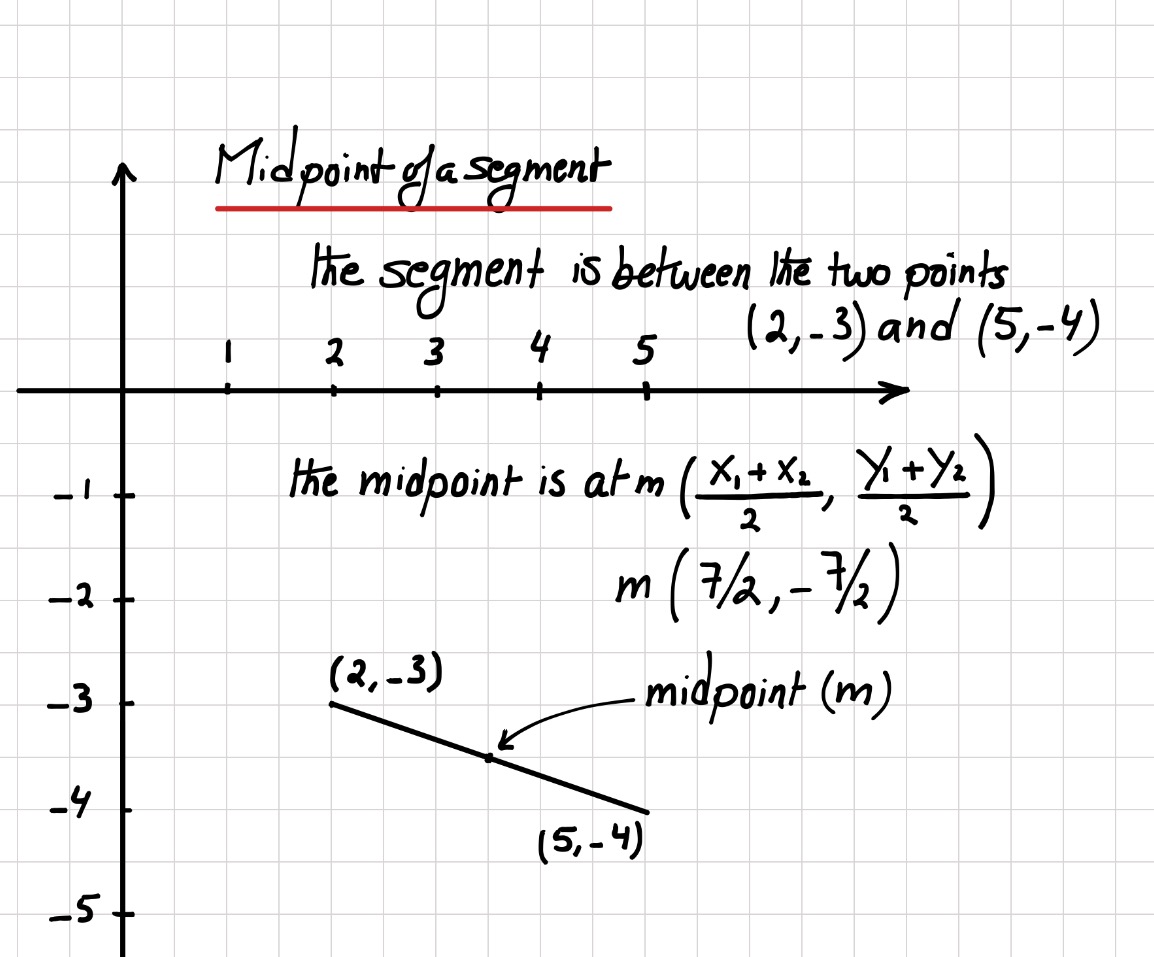
How do you integrate a line segment. I am trying to use contour integration to find the integral of: If \(c\) is a curve, then the length of \(c\) is \(\displaystyle \int_c \,ds\). $$ \int_\gamma ydz $$ where we have the union of line segments from $0$ to $i$ and then to $i+2$.
The line integral $\int_c \nabla f \cdot d\textbf{r}$ is by definition $\int_c \nabla f \cdot \textbf{n} \ ds$, where $\textbf{n}$ is a unit tangent vector to the curve $c$ at every. An open path is just your typical line integral that you know and love, the only difference for the closed version is the endpoints a and b coincide. I want to find $$\int_c (x^2 dx + y^2 dy + z^2 dz),$$ where $c$ is the curve consisting of line segments from $(0,1,0)$ to $(1,0,1)$ and then from $(1,0,1)$ to.
The line integral of \(f\) with respect to \(x\) is, \[\int\limits_{c}{{f\left( {x,y} \right)\,dx}} = \int_{{\,a}}^{{\,b}}{{f\left( {x\left( t \right),y\left( t \right)} \right)x'\left( t \right)\,dt}}\] Well, the steps are really quite. The line integral through a vector field gets multiplied by − 1 when you reverse the orientation of a curve.
We’ll start with the vector field, →f(x, y, z) = p(x, y, z)→i + q(x, y, z)→j + r(x, y, z)→k. First, change \(\vec{a}\) into \(\dfrac{dv}{dt}\) (the.
Using each line segment as the base of a rectangle, we choose the height to be the height of the surface $f$ above the line segment. With line integrals we will be integrating functions of two or more variables where the independent variables now are defined by curves rather than regions as with. To get work over a line, the end result should be \(\int_c \vec{f} dr\), the sum of the forces over the line \(r(t)\).
How to use this line integral formula to find the work done by a vector field or force field \(\vec f\) in moving an object along a vector? If we add up the areas of these rectangles,. In this video, i evaluate a line integral along a straight line segment by using a parametric representation of the curve (using a vector representation of the line.
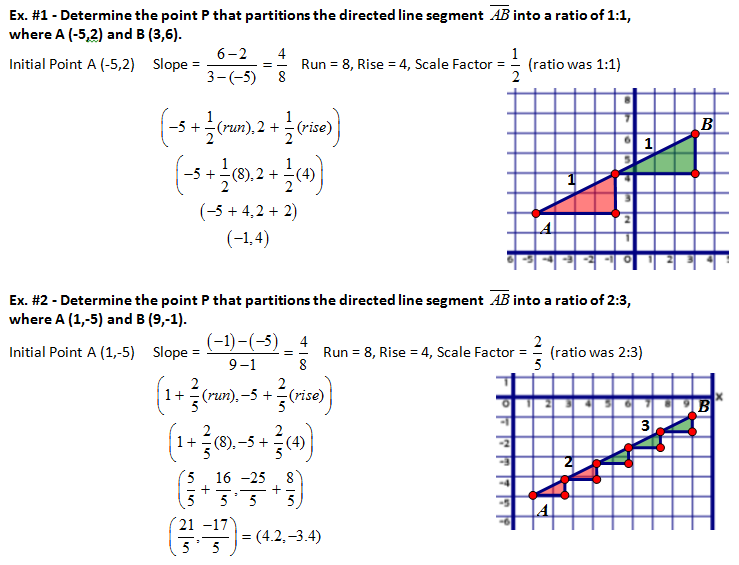
![[Math] Line Integral Along A Straight Line Math Solves Everything](https://i.stack.imgur.com/Xx5LE.png)