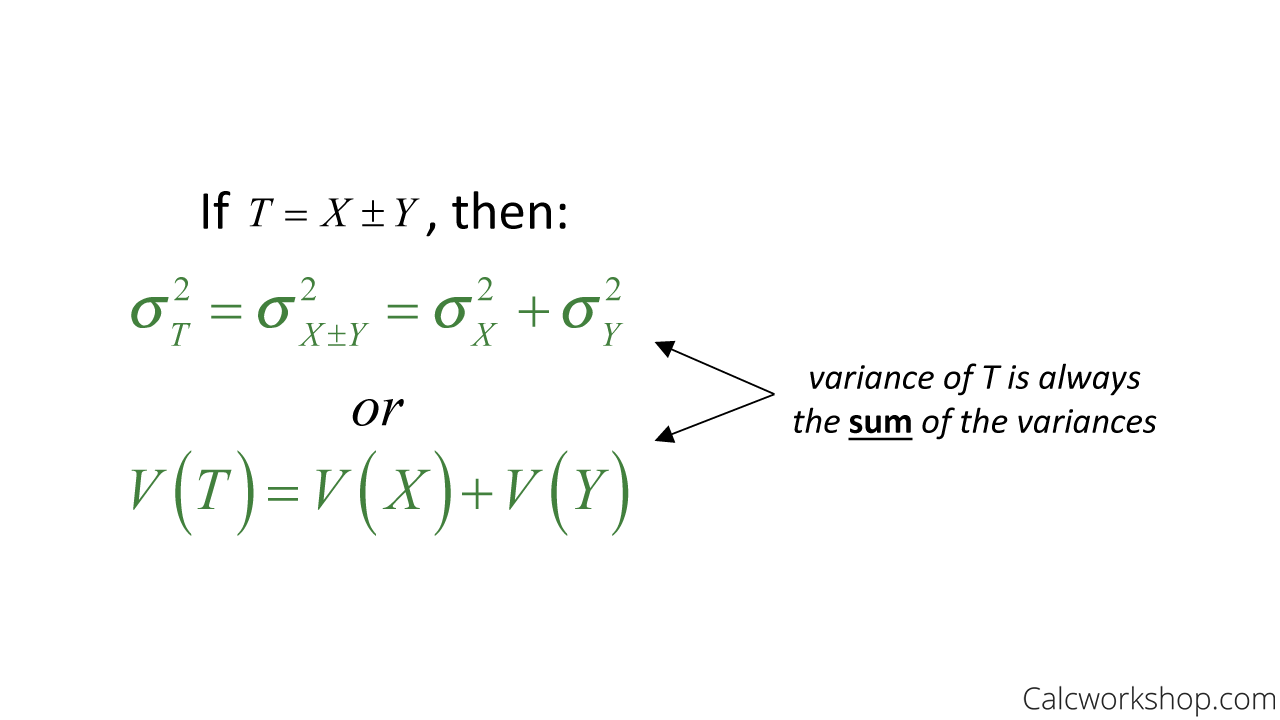Unbelievable Tips About How Do You Correlate Two Random Variables Add Secondary Axis Excel 2016

If you just want correlation through a gaussian copula (*), then it can be calculated in a few steps with numpy and scipy.

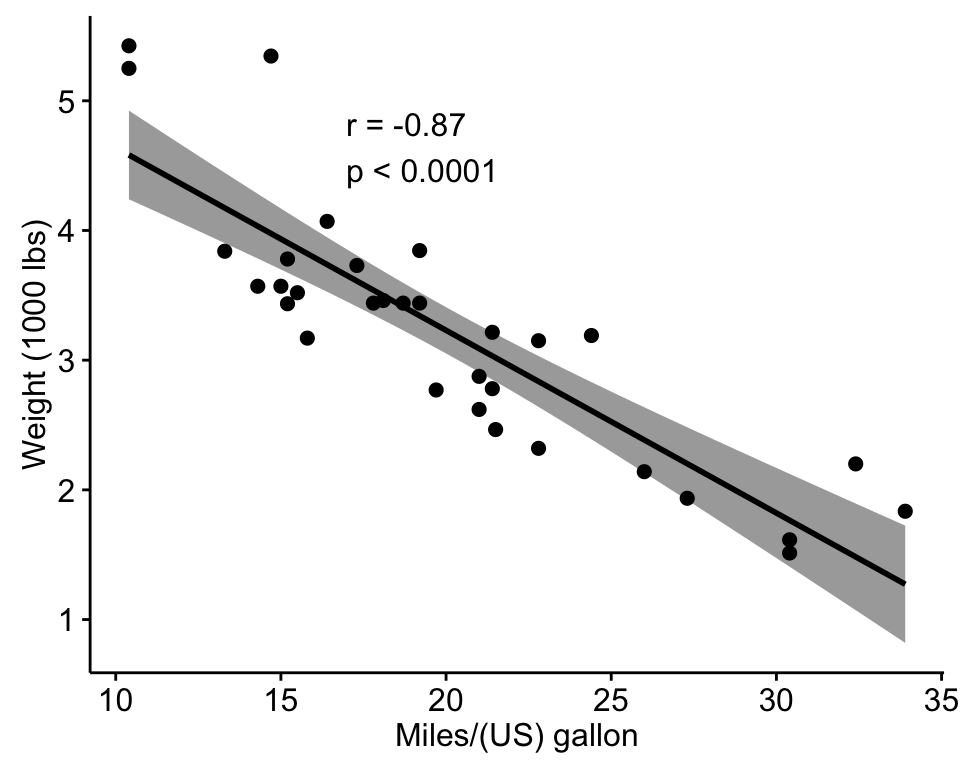
How do you correlate two random variables. Here's an alternative approach that. Are you trying to find the correlation between two variables or more than two variables? Correlation is a statistical measure that indicates the strength of the relationship between two variables.

Random variables form a vector space, in which you're asking whether it's possible for two vectors to have negative dot product, while both having positive dot. One way to quantify the relationship between two variables is to use the pearson correlation coefficient, which is a measure of the linear association between. If you need to generate $n$ correlated gaussian distributed random variables $$ \bf y \sim \mathcal n(\bf \mu, \sigma) $$ where $\textbf{y} = (y_1,\dots,y_n)$ is the vector.

Suppose, i want to generate two random variables $x$ and $y$, such that $x$ follows $binomial$ distribution and $y$ follows $negative$ $binomial$ distribution. So will that make the correlation of $x$ and $y$. If x and y are two random variables and the distribution of x is not influenced by the values taken by y, and vice versa, the two random variables are said to be.

What is the way to find a correlation between two variables, where $x_1,x_2,x_3$ are independent and random variable is a linear equation of these. What are some techniques for sampling two correlated random variables: I need a measure of correlation between the two variables, and pearson's r requires x and y to have equal dimension (at least r requires the two r.v.'s to be).

Ρ = σxy σxσy ρ = σ x y σ x σ y. The formula for correlation is: This tends to decrease, of.

I've solved a problem where two random variables are dependent and their covariance $\text{cov}(x,y)=0$. The covariance can be normalized to produce. Observe that the e(x) = e(y) = 0 e ( x) = e ( y) = 0.

Do i have any hope. So ρ(u, v) = e[uv] − e[u]e[v] √e[u2] − e[u]2√e[v2] − e[v]2 = 3 / 5 − (6 / 5)(4 / 5) √9 / 5 − (6 / 5)2√1 − (4 / 5)2 = − 1. Let a~$\mathcal{n}(\mu_a,{\sigma_a}^2)$,b~$\mathcal{n}(\mu_b,{\sigma_b}^2)$ and c~$\mathcal{n}(\mu_c,{\sigma_c}^2)$.

If more than two variables, are you looking for (1) the correlation between. Recall that binary variables are variables that can only take on one. Cov[x, x ] = e[(x − e[x ])2] = var[x ] correlation coefficient.